Symbolic-Processor
1. Abstract
This white-paper explains the concepts behing a symbolic-processor which is a putative new application-type with a universal data-model. This spectral data-model embraces all data, wherever stored, and in whatever format. It does this by converting all such data into a local "Trie" data-structure. This spreadsheet includes a working proof-of-concept that the user can explore.
It first examines the 4 principles behind a symbolic-processor; no mathematical-Platonism, the spectral data-model, combinatory binary-operations, and no explicit loops, routines or if/then statements. It then deep-dives into the data, processing and sequencing requirements of a symbolic-processor, uses examples to highlight how it improves-upon conventional programming-languages (e.g. no loops required in calculating a standard-deviation), before addressing future developments.
2. Problem Statement
The issue is principally one of there currently being a ""tower-of-Babel"" when it comes to computer-programming-languages; why are there so many, why are they so different, and why are they all so complex? (loops, functions, reals, strings, if/then statements, etc.). Also, why can't IT be the same as simple school-arithmetic which uses a single language everywhere? (e.g. 1 + 2 = 3 etc.).

The Tower of Babel (Bruegel the elder, circa 1560), a previous (failed) approach to language unification.
3. Background
AGD Research has focused its' endeavours towards the deeper, more fundamental aspects of problems in IT, which inevitably then "spill-over" into mathematics, and even philosophy! Programming-languages fit this pattern; the complexity of IT languages contrasted with arithmetic's simplicity, then arithmetic itself being extended, forcing the "ditching" of mathematical-Platonism (philosophy). Surprisingly perhaps, this fundamental research has resulted in 2 ideas with significant economic potential; a symbolic-processor, and especially its universal data-model (the spectral data-model).
4. Solution
The approach AGD Research took in exploring how programming-languages might be simplified is to start from the simple and universal language of school-arithmetic (e.g. 1 + 2 = 3 etc.), see if this can be extended into programming-languages, and establish how far? All the way is the surprising answer, but it necessitates a new type of application (a symbolic-processor), and language (a symbolic-processing-language; acronym an SPL). This proof-of-concept interprets the SPL, but ideally it would be compiled, perhaps even in real-time as the VBA programming-language is.
4.1. The 4 Attributes of a Symbolic-Processor
In extending the notation of arithmetic to encompass computer-programming 4 defining attributes of a symbolic-processor have been identified.
4.1.1. No Mathematical-Platonism
For a symbolic-processor to have just a single type of data, symbolic-strings, that means traditional numbers, variable-names, text and all the current myriad of other types (the data-type "zoo") have to be treated identically. That means numbers are the same as text are the same as variable-names etc. In turn that means text can legitimately occur in arithmetic operations, e.g. 1 + two = 3, and this certainly "breaks-the-old-rules". In this example 1 + two returns a symbolic-string of length zero (i.e. nothing), and nothing is not-equal to 3, so 0 is returned (false).

In a symbolic-processor, symbols do not refer to any deeper reality, they just represent themselves.
4.1.2. Spectral Data-Model
Firstly, for there to be a single data-type, the problem of being able to refer to data (the variable reference name), rather than the data itself, must be addressed. A symbolic-processor does this via the spectral data-model. In this model there is no difference between data and its reference name. The "trick" is to front-end the data with its' reference, as in CurrentYear2022 where CurrentYear takes the place of the key (the value is known), and 2022 the data (the value is unknown). It is known as the spectral data-model because in general there is no hard cut-off between key and data; instead the known (towards the left of a symbolic-string and spectrum = blue) drifts into the unknown (towards the right of a symbolic-string and spectrum = red), as in CurrentYear2022. The key, the data (attributes), or any combination of the 2 can be returned by using wild-cards in the search. If multiple symbolic-strings are considered together (e.g. CurrentYear2022, CurrentMonthJuly, CurrentDay22 etc.), they can be represented as an STree (spectral or sparse tree).
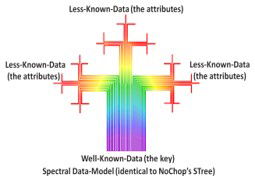
Representation of an STrie. At each bend the data diverges.
Secondly, for there to be a single data-type, the problem of where the data is being held must be addressed. Is the data in-memory, on disk, in a database, in the cloud, in an application or somewhere else? A symbolic-processor resolves this by scanning each symbolic-string looking for \ signs; if there are none the data is in-memory, if there are it will attempt to locate data on a disk or in the cloud (e.g. C:\SymbolicProcessor\Data\CurrentYear2022), or if enabled, data in an external application (this proof-of-concept has enabled key aspects of Excel; values, formulae, tabs, colours etc.). This is potentially very powerful; a common way of reading-and-writing data to-and-from any application, anywhere (i.e. commoditizing data). Companies and organizations that enable this commoditization would see economic benefits accrue to themselves and away from individual providers such as databases, ERP solutions, etc. Virtual layers can also be incorporated to control access-security (e.g. C:\Excels\ACME-P&L\Password\qwerty123\A1\1\Channel).
4.1.3. Combinatorial Binary-Operations
All operations in a symbolic-processor are binary, with the single exception of the read-operation which utilizes wild-cards and filters ("principes zijn zoals scheten; als je ze niet kunt houden, moet je ze laten gaan" - a rough translation from the Flemmish being ""occasionally you have to let-go of a principle"") . Binary-operations have 1 operator, 2 input operands and 1 output as in 1 + 2 which returns 3. These operations can be combined in various combinations across symbolic-strings to produce bijections and various Cartesian-products by repeating the operator-symbol (e.g. +++ or 3+ for short):
1 2 + 3 4 5 returns 1 5 4 5 (example standard)
1 2 ++ 3 4 5 returns 4 6 (example bijection)
1 2 +++ 3 4 5 returns 13 14 (example Cartesian-accumulate)
1 2 ++++ 3 4 5 returns 4 8 13 5 9 14 (example Cartesian-carry)
1 2 +++++ 3 4 5 returns 4 5 6 5 6 7 (example Cartesian-classic)
Note that the repeating operator-symbol can be shortened by prefixing the number of occurrences (e.g 3+ is equivalent to +++).
4.1.4. No Explicit Loops, Routines or If/Then Statements etc.
The functionality above mostly removes the need for a symbolic-processor to have explicit loops, routines or if/then statements. More fundamental operations (comparison and replication) can be used to provide this implicit functionality if required. Likewise, Boolean "And"s and "Or"s are modelled by the multiplication and addition of 0's and 1's. For "And"s (1 > 0) * (1 = 1) = 1 returns 1 (true), but (1 > 0) * (1 = 0) = 1 returns 0 (false). For "Or"s (1 > 0) + (1 = 0) > 0 returns 1 (true), but (1 > 1) + (1 = 0) > 0 returns 0 (false). Comments can be accomplished by code that always returns nothing, as in (0 ? [this is an example of a comment in the code]).
4.2. Data
In a symbolic-processor any symbolic-string that is not an operator (e.g. +, **, = etc.) is data. These comes in 2 forms; unboxed and boxed (see below), which explains why this section is so short. As there is only 1 data-type (the symbolic-string), no ""casting"" between different data-types is needed (i.e. no conversions are required). This is the antithesis of (and ""antidote"" to), the vast majority of current/popular computer-languages (e.g. Python, C etc.) where ""strong-typing"" is the norm. Note - some computer-languages even allow the user to create their own data-types (user-defined complexity?)
4.2.1. Unboxed Symbolic-Strings
These are "raw" symbolic-strings, not protected by being boxed, and form the familiar objects of a programming-language. A user can regard the symbolic-string 123 as an integer, 123.45 as a real, 0 as a Boolean, CurrentYear as a text, aaa.bbb@ccc.ddd as a URL, but to a symbolic-processor they are just variants of a single data-type, an unboxed symbolic-string.
4.2.2. Boxed Symbolic-Strings
These are symbolic-strings, including operators, that are protected by being boxed (a box is represented by matching square-brackets, e.g. [1 + 2 = 3] etc.). Boxes can be embedded in other symbolic-strings (e.g. Hundred[10 * 10] etc.), and can even be nested (e.g. Hundred[10 * [2 * 5]] etc.).
4.2.3. The Symbolic-String Line and Rectangle
Unlike the real-numbers in mathematics, symbolic-strings cannot be properly represented as single points on a line. This is because under ""<"" (less-than operator) ordering (see Comparison operators below), there are equivalent numeric symbolic-strings (strings that a user would identify as a number) that occupy the same position on the line (e.g. 6 = 06 = 6.00 and 0 = 00 = 0.00 = -0 etc.). Text symbolic-strings can be represented as points on a line. If however, numeric symbolic-strings are restricted to their minimum-forms, they can be represented as single points on a line (a numeric minimum-form has no leading or trailing zeros, e.g. 6 or 0, but an equivalent-form does have leading and/or trailing zeros, e.g. 06 or 6.00 or 00 or 0.00 or -0 etc.). To easily convert between one equivalent-form to another the "~" (truncate operator) can be used, as in 6.00 ~ 0 returns 6, 6 ~ 2 returns 6.00, 06 ~ -1 returns 6 and 6 ~ -2 returns 06 etc. Also, to easily convert an equivalent-form to its minimum-form just add 0 (zero) to it, e.g. 06 + 0 returns 6, 6.00 + 0 returns 6 and -0 + 0 returns 0 (see Arithmetic operators below).
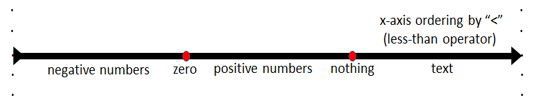
The Symbolic-String Line(minimal-forms only).
If however the symbolic-string line is extended to form a rectangle, with the x-axis representing an ordering by "<" and the y-axis representing an ordering by "<" of equivalents via their boxed-forms, a proper representation can be obtained (a boxed-form of 6 is [6], of 06 is [06], of 6.00 is [6.00], of 0 is [0], of 00 is [00], of 0.00 is [0.00] and of -0 is [-0] etc.). Traversing this rectangle from left-to-right returns symbolic-strings that are negatives followed by zeros followed by positives followed by nothing (a symbolic string of length zero) followed by text. In a more set-theory orientated notation this is {negatives} then {0's} then {positives} then {} (nothing: the empty-set) then {text}. This ordering provides a simple way to differentiate between numbers and text: {numbers} are < than {} (nothing), and {text} is > than {}.
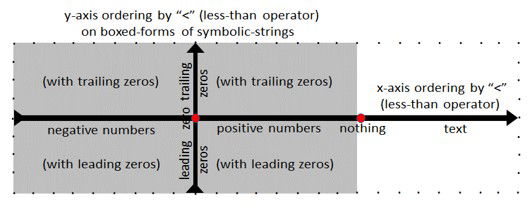
The Symbolic-String Rectangle(all-forms: minimal and equivalents).
4.3. Processing
In a symbolic-processor operators fall in a number of distinct classes; reads, writes, arithmetic, comparisons etc. These are explained below:
4.3.1. Reads
4.3.1.1. Wild-Cards
* string (e.g. if in-memory, CurrentYear* returns CurrentYear2022, Current*22 returns CurrentDay22 CurrentYear2022 and C*t* returns CurrentDay22 CurrentMonth07 CurrentYear2022 etc.)
? symbol (e.g. if in-memory, Cu?entYear* returns nothing, Cu??entYear* returns CurrentYear2022, Cu???entYear* returns nothing and ?* returns everything in-memory etc.)
| alphabetic (e.g. if in-memory, CurrentYear202| returns nothing and CurrentYear202! returns CurrentYear2022 etc.)
! numeric (e.g. if in-memory, CurrentYear202! returns CurrentYear2022 and CurrentYear202! returns nothing etc.)
4.3.1.2. Filters
= equals (e.g. if in-memory, CurrentYear=2022 returns CurrentYear2022, CurrentYear=2021=2022 returns nothing ("and" logic) and CurrentYear=2021*=2022 returns CurrentYear2022 ("or" logic) etc.)
# not-equals (e.g. if in-memory, CurrentYear#2022 returns nothing, CurrentYear#2021#2022 returns nothing ("and" logic) and CurrentYear#2021*#2022 returns CurrentYear2022 ("or" logic) etc.)
> greater (e.g. if in-memory, CurrentYear>2022 returns nothing, CurrentYear>2021>2022 returns nothing ("and" logic) and CurrentYear>2021*>2022 returns CurrentYear2022 ("or" logic) etc.)
} greater-or-equal (e.g. if in-memory, CurrentYear}2022 returns CurrentYear2022, CurrentYear}2021}2022 returns CurrentYear2022 ("and" logic) and CurrentYear}2021*}2022 returns CurrentYear2022 ("or" logic) etc.)
< less (e.g. if in-memory, CurrentYear<2022 returns nothing, CurrentYear<2021<2022 returns nothing ("and" logic) and CurrentYear<2021*<2022 returns nothing ("or" logic) etc.)
{ less-or-equal (e.g. if in-memory, CurrentYear{2022 returns CurrentYear2022, CurrentYear{2021{2022 returns nothing ("and" logic) and CurrentYear{2021*{2022 returns CurrentYear2022 ("or" logic) etc.)
4.3.1.3. Mask
" toggle (e.g. if in-memory, CurrentYear* returns CurrentYear2022, CurrentYear"* returns CurrentYear, "CurrentYear"* returns 2022 and Current"Year"* returns Current 2022 etc.)
4.3.2. Writes
| upsert (e.g. CurrentYear | 2022 creates CurrentYear2022 in-memory having deleted any-and-all existing symbolic-strings beginning CurrentYear and | deletes everything in-memory)
! delsert (e.g. CurrentMonthJune ! CurrentMonthJuly deletes in-memory the June symbolic-string if it exists, then inserts the July one if that does not. Spaces force pure deletes or inserts)
Note that "upsert" is an elision of "update" and "insert", and "delsert" an elision of "delete" and "insert". These 2 operators provide the equivalent functionality of "insert", "update" and "delete"in traditional data-manipulation-languages such as SQL.
4.3.3. Arithmetic
+ add (e.g. 1 + 2 returns 3, 1.2 + 3.4 returns 4.6 and 1.2 + ThreePointFour returns nothing, etc.)
- subtract (e.g. 1 - 2 returns -1, 1.2 - 3.4 returns -2.2 and 1.2 - ThreePointFour returns nothing, etc.)
* multiply (e.g. 1 * 2 returns 2, 1.2 * 3.4 returns 4.08 and 1.2 * ThreePointFour returns nothing, etc.)
/ divide (e.g. 1 / 2 returns 0.5, 1.2 / 3.4 returns 0.352941176470588, 1.2 / ThreePointFour returns nothing and 1.23 / 0 also returns nothing, etc.)
^ exponentiate (e.g. 1 ^ 2 returns 1, 1.2 ^ 3.4 returns 1.85872969197948 and 1.2 ^ ThreePointFour returns nothing, etc.)
~ truncate (e.g. 12.34 ~ 0 returns 12, 1.23 ~ 1 returns 1.2, 1.23 ~ 4 returns 1.2300, 12.34 ~ -0 returns 0.34, 12.34 ~ -1 returns 2.34, 12.34 - 3 returns 012.34 and ThreePointFour ~ 0 returns nothing, etc.)
Note that using all the above operators returns a symbolic-string in its minimum-form (e.g. 1.20 + 3.000 returns 4.2 and 02.00 ^ 3.0 returns 8).
4.3.4. Comparisons
= equal (e.g. 1 = 2 returns 0, 1.2 = 1.20 returns 1, Xxx = Xxx returns 1, Xxx = xxx returns 0, = 0 returns 0 and 1.2 = OnePointTwo returns 0, etc.)
# not-equal (e.g. 1 # 2 returns 1, 1.2 # 1.20 returns 0, Xxx # Xxx returns 0, Xxx # xxx returns 1, # 0 returns 1 and 1.2 # OnePointTwo returns 1, etc.)
> greater (e.g. 1 > 1 returns 0, 1.23 > 1.20 returns 1, Xxx > 1.23 returns 1, Xxx > xxx returns 0, > 0 returns 1 and 1.2 > OnePointTwo returns 0, etc.)
} greater-or-equal (e.g. 1 } 1 returns 1, 1.23 } 1.20 returns 1, Xxx } 1.23 returns 1, Xxx } xxx returns 0, } 0 returns 1 and 1.2 } OnePointTwo returns 0, etc.)
< less (e.g. 1 < 1 returns 0, 1.23 < 1.20 returns 0, Xxx < 1.23 returns 0, Xxx < xxx returns 1, < 0 returns 0 and 1.2 < OnePointTwo returns 1, etc.)
{ less-or-equal (e.g. 1 { 1 returns 1, 1.23 { 1.20 returns 0, Xxx { 1.23 returns 0, Xxx { xxx returns 1, { 0 returns 0 and 1.2 { OnePointTwo returns 1, etc.)
Note that a Symbolic-Processor differentiates between the "equals" comparison (represented by the = symbol) and the "same-as" comparison (which has no symbolic representation). The "same-as" comparison can be accomplished by first "boxing" the operands via the & (amass) operator (see below). So 0 = -0 returns 1, but (& 0) = (& -0) returns 0 (i.e. [0] does-not-equal [-0]).
4.3.5. Appends
& amass (e.g. 1 & 2 returns [1 2], 1 & [2 3] returns [1 2 3], [1 + 2] & 3 returns [1 + 2 3], [1 +] & [2 = 3] returns [1 + 2 = 3], & 0 returns [0] and [[1]] & Two returns [[1] & Two], etc.)
@ attach (e.g. 1 @ 2 returns 12, 1 @ [2 3] returns 1[2 3], [1 + 2] @ 3 returns [1 + 2]3, [1 +] @ [2 = 3] returns [1 +][2 = 3], @ 0 returns 0 and 1 & Two returns 1Two, etc.)
; avoid (e.g. 1 ; 2 returns 1 2, 1 ; [2 3] returns 1 [2 3], [1 + 2] ; 3 returns [1 + 2] 3, [1 +] ; [2 = 3] returns [1 +] [2 = 3], ; 0 returns 0 and 1 & Two returns 1 Two, etc.)
4.3.6. Manipulation
? replicate (e.g. 0 ? Xxx returns nothing, 1 ? Xxx returns Xxx, 2 ? [3 + 4] returns 7 7, -1 ? Xxx returns Xxx, -2 ? [3 + 4] returns [3 + 4] [3 + 4], and Xxx ? One returns nothing, etc.)
$ select (e.g. M8 $ 0 returns 2, M8 $ 00 returns M 8, M8 $ 2 returns 8, [M 8] $ 0 returns 2, [M 8] $ 00 returns M 8, [M 8] $ 2 returns 8, M8[M 8] $ 0 returns nothing, M8[M 8] $ 2 returns nothing, M8[M 8] $ -0 returns 2, M8[M 8] $ -00 returns M8 [M 8] and M8[M 8] $ -2 returns [M 8] etc.)
% partition (e.g. Abc $ 0 returns 3, Abc $ 1 returns A, Abc $ 2 returns b, Abc[def] $ -0 returns 2, Abc[def] $ -1 returns Abc and Abc[def] $ -2 returns [def] etc.)
4.4. Sequencing
default order-of-precedence: first process read-operations, then arithmetic1 (*/^~), then arithmetic2 (+-), and last all-others (e.g. if in-memory, 1 @ 2 + 3 * "CurrentYear"* returns 16068 and not 30300 etc.)
() override (e.g. 1 + (2 * 3) returns 7, (1 + 2) * 3 returns 9, Day(1 2) returns Day1 Day2, A(1 2 3)Z returns A1Z A2Z A3Z, (A Z)(1 2) returns A1 A2 Z1 Z2 and ((1 + 2) * 3)Nine returns 9Nine etc.)
5. Examples
A standard-deviation, and the spectral-data-model applied to an Excel spreadsheet (please download the Symbolic-Processor from the Downloads page to try-out these examples).
5.1. Standard-Deviation: Symbolic-Processor (5 lines of code; zero loops), versus the C computer-language (25 lines of code, 3 loops)
Copy the single line below, open-up the symbolic-processor CMD-prompt popup, then paste into the CMD-prompt and enter.
StdDevSample | [50 40 60 50 70 30 20 50 60 50]
Copy the 5 lines below, then paste into the CMD-prompt and enter.
StdDevMeanSample | (0 +++ "StdDevSample"* $ 00) / ("StdDevSample"* $ 0) ;
StdDevErrorsRaw | (3& ("StdDevSample"* $ 00 5- "StdDevMeanSample"*)) ;
StdDevErrorsSquared | (&&& ("StdDevErrorsRaw"* $ 00 ** "StdDevErrorsRaw"* $ 00)) ;
StdDevMeanSquaredError | ((0 +++ "StdDevErrorsSquared"* $ 00) / (("StdDevSample"* $ 0) - 1)) ;
"StdDevMeanSquaredError"* ^ 0.5

Standard-Deviation example using the CMD-prompt popup.
To better "industrialize" this example, the code can be kept in a flat-file then executed. Open a text-editor (e.g. Notepad etc.), copy-and-paste the same 5 lines of code, and save it. Then in the CMD-prompt enter a new sample (e.g. StdDevSample | [60 40 60 20 70 30 20 50 60 40]). Then enter the appropriate file-based replicate-operation (e.g. 1 ? "C:\SymbolicProcessor\Data\StdDev.txt"*).

Standard-Deviation example using a file-based code.
The equivalent C computer-program (25 lines of code; 3 loops)
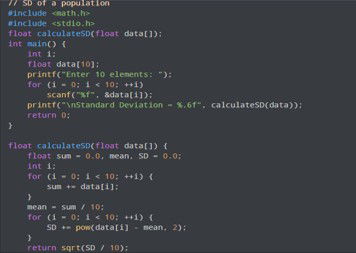
This C code is taken from an on-line class-library.It is 25 lines long and requires 3 loops.
The above C code is 25 lines long and requires 3 loops, while the SPL (symboli- processo- language) code is just 5 lines long and requires no loops. This reduction is due to SPL being able to handle objects at both an individual level and as a collection of them. However, a symbolic-processor can also support "open-ended" loops and if/then statements if absolutely required (loops with an indeterminate number of iterations). A loop structure can be constructed via recursion. Copy-and-paste the single-line below into the CMD-prompt and enter. Then enter Count* to check the code worked. Note that this recursion will not "blow-the-stack" if the interpreter/compiler has been written correctly, as indeed this proof-of-concept has been).
Count | 0 ; TestLoop | [Count | "Count"* + 1 ; "Count"* < 100 ? "TestLoop"*] ; 1 ? "TestLoop"*
In the aboce SPL code the "?" (replicate operator) is used as a proxy to an "if" statement in traditional computer-languages. If the number of replications specified is 0 (zero/false) then no (boxed) symbolic-string is returned, and so its operations are not performed. If the number of replications is 1 (one/true), then the operations are performed. Recursion is used as a proxy to a "for" statement in traditional computer-languages (i.e. each recursion is equivalent to an iteration).
5.2. Spectral-Data-Model (as applied to an Excel spreadsheet)
This Excel spreadsheet has been partially enabled for the spectral-data-model. Below is a table of what has been enabled so far.
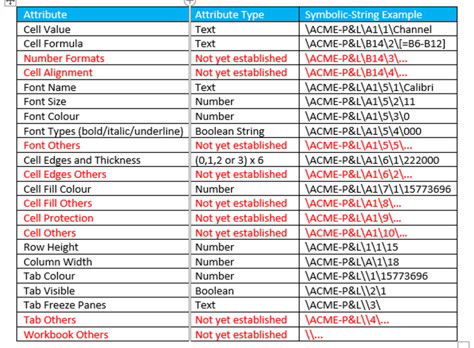
Table showing the keys and attributes of Excel enabled spectral-data-model.
6. Future Developments
The "call-to-arms" is for the ideas laid-out here to be adopted, in full or in part. Although this symbolic-processor is a proof-of-concept, which AGD Research believes has been a success, in development terms it is likely that these are adopted piecemeal. In particular 2 ideas might have near-term utility in existing environments (e.g. programming, command-lines etc.); the use of wild-cards and filters for in-memory retrievals (e.g. "Count"* etc.), and combinatorial binary-operations (e.g. 1 2 ++ 3 4 etc.). Longer term the spectral data-model may have significant impact in commoditizing data (i.e. enabling applications and databases so the can be accessed-and-maintained according to a universal standard).
7. References
(Wikipedia) https://en.wikipedia.org/wiki/Philosophy_of_mathematics#Platonism
(Wikipedia) https://en.wikipedia.org/wiki/Trie
(AGD-Research) https://agdresearch.com/home
| 8. Author Andrew Guthrie-Dow, AGD-Research, January 2025 |