STrie-vs-Quick-Sort

1. Abstract
This white-paper contrasts-and-compares the supremacy of the STrie algorithm (a variant of TRie developed in 2019) against the QuickSort algorithm (developed in 1960). QuickSort is still widely perceived as being the fastest sort algorithm in existence (QuickSort when well implemented being faster than its 2 current rivals of MergeSort and HeapSort). Using simple mathematics this white-paper derives a speed formula for STrie that is up to 8 times faster than the equivalent formulae of QuickSort, MergeSort and HeapSort.
It first explains how-and-why a sort algorithm developed in the 21st century might very well be faster than those developed in the 20th century (modern computers have resources such as vast-memory and access speeds unthinkable in the 1960's). It then further examines the structure of real-world data and explores what types of algorithm might be best suited to exploit this structure. It then exposes and analyses the same hidden procedure/assumption embedded in the QuickSort, MergeSort, BinaryChop and BTree algorithms that restrict their performance to the same upper speed-limit (please note that RadialSort also avoids this hidden assumption). It then details the STrie algorithm itself and explains how it avoids this upper limit. It then derives a new speed limit formula that is up to 8 times faster than these competitor algorithms. It then explores and identifies the "downsides/watchouts" of using STrie before addressing future developments. Finally there are references to aid further research-and-development.
2. Problem Statement.
The issue is principally one of speed. All deep-stack algorithms (ones used as components of higher level applications) should be under constant review to see if they can be made to run faster, or be replaced entirely by something that can. Any improvement in sort-run-times would be readily adopted within IT, and significant efficiencies gained (e.g. faster batch run times, faster collation of data, faster algorithms with embedded sorts, etc.).
Speed/efficiency is everything. Speed can be converted into money, time, carbon-offsets, or whatever. A better algorithm delivers immediate benefits to everyone; a quick-and-easy "win-win" for all.
3. Background
The STrie algorithm was not developed as either a sort algorithm or a data-retrieval-and-storage algorithm. Instead it emerged as a bi-product of another proposed development; a symbolic-processor. The STrie fast-internal-memory data-structure is a component of a symbolic-processor and follows its universal "spectral" data-model. Although AGD Research was not astute enough to create and understand STrie from first principles, with outside direction, its potential in a wider IT context has now been quantified and demonstrated.
4. Solution
The solution is split into 5 sub-sections; advances since the 1950's, structures within data that can be leveraged, the STrie algoritm in detail and how it avoids a critical hidden assumption in its competitor algorithms, the mathematics underlying its performance, and downsides and watch-outs.
4.1 Advances since the 1960's
Any algorithm, regardless of how clever, stupid, elegant or brutal it is, uses a limited number of available resources. These are the ability to write data, to read data, to compare data and to manipulate data. In the last century when STries's competitor algorithms were developed, all of these 4 resources were at a premium, but especially the ability to read and write data quickly and in large volumes. Hence only those algorithms that were "easy" on these resources would thrive.
In recent years with new technologies none of these resources pose the same bottlenecks as before. This opens-up the possibility that an algorithm may do a "deal-with-the-devil" where vast amounts of these cheap resources are sacrificed in the name of speed. This is precisely what STrie does; it utilizes sizeable amounts of computer memory and processing, far more than its competitors, but delivers the results more quickly.
4.2. Real-World data
Most data that any sort algorithm will encounter is encoded according to the ASCII standard. This standard is itself embedded in the last century as can be seen in its coding structure. The first 32 symbols were envisaged as control symbols for teletype machines with characters for carriage-return, line-feed, and even ringing the bell. Then the next 32 symbols contained various punctuation marks and the digits 0 to 9. The 32 symbols after that contained the upper-case letters and some more puctuation marks. The 32 symbols after that contained the lower-case letters and yet more punctuation marks. Finally the last 128 characters were left open for local symbols such as Scandinavian characters.
Typically data that needs to be sorted will be very clustered within the 256 symbols of the ASCII standard. It will be very rare for any human-centric data to be in the first 32 characters (the control characters). Numeric data will cluster in the symbols between 33 to 64. Names, addresses and identifiers where the leading symbol is upper-case will cluster in symbols 65 to 96. Lower-case data such as words will cluster in symbols between 97 to 132. Finally certain data-sets, such as for Scandinavian character-sets, will cluster in symbols between 133 to 256.
STrie when being used as a sort engine comes in 2 phases; a sparse-matrix build followed by a sparse-matrix read (the details of this sparse-matrix are in the followng sub-section). The sparse-matrix is composed of columns which represent the 256 ASCII characters and rows that represent branches in a tree-structure. The number of rows tends to be somewhat larger than the number of keys/entries that are being sorted. The sparse-matrix build is very efficient as the STrie algorithm ensures there are no surprise collisions due to hashing. However the sparse-matrix read would be inefficient if it had to read every entry. Instead during the build phase additional meta-data marks for each row which position to start from and which to finish at for dense data, and individual points for occasional-data (3 or less points), or a mix (in a mix STrie always places individual points to the right of continuous ones as outliers are more likely towards the end of the alphabet as it was extended historically to include symbols such as w, x, y and z, and beyond these into the ""exotic"" characters between 128 and 255). This extra data is metametadata (data about data about data).

STrie's Sparse-Matrix showing typical "go-faster" striping metadata.
4.3. Hidden Speed-Limiting Procedure/Assumption Shared by QuickSort, MergeSort, HeapSort, BinaryChop and BTree.
The hidden procedure/assumption in the above algorithms is that the only way to achieve a sort, a read or a write is to compare the whole key/entry with something else, such as another whole key/entry, then depending on the result, move or swop data. Indeed the BinarySearch algorithm makes this clear in its name. This procedure/assumption leads to an inevitable logic-chain that results in a sorting speed limited by O (n log(n)) where n is the number of keys/entries, and O (log(n)) for data-retrieval-and-storage (the big "O" notation simply means the limiting function as n tends to infinity, without worrying about minor terms etc.)
As an example the QuickSort algorithm first splits all the keys/entries into 2 sub-sets, each key/entry in the first sub-set being less than each key/entry in the second sub-set. It then repeats this splitting on these 2 sub-sets, then on the 4 sub-sub-sets of the first 2 sub-sets, and so on until the sub-set size is so small it can only contain a single key/entry, and the sort is completed. If we follow the "life" of a single entry during QuickSort we can see it has to go through a comparison and potential move/swop for each sub-set and sub-sub-set etc. Therfore the sort time for an individual key/entry is directly related to the number of partitioning-levels it has to go through. Mathematically this is saying the total-number of keys/entries is 2-to-the-power of the number-of-levels, or n = 2 ^ p. This equation can be solved by using the inverse log function (to the base 2), giving a limiting-time for an individual key/entry of log(n). As there are n keys/entries, the final speed-limiting function is n log(n).
Attempts at amending the algorithms of STrie's competitors to break this speed-limit by splitting keys/entries into more than 2 piles at each level fail. Assigning a key/entry into more than 2 piles would require some "magic" method of doing this as comparisons are binary, not tertiary or whatever. How STrie avoids this trap is that its sub-keys/sub-entries automatically partition into piles of up to 256, their positions within each pile being the ASCII code of the first character of each sub-key/sub-entry. The "magic" is baked-in (the multi-partitioning is already coded in the key/entry)!
4.4. The STrie Algorithm
STrie avoids the above speed-limit because instead of comparing one whole key/entry with another whole key/entry, then taking some action, it decomposes each individual key/entry into sub-keys/entries and processes those to perform a sort. It does this by building a tree-structure consisting of a 2-dimensional integer sparse-matrix and a 1-dimensional string-array that represents, in pieces, all the individual whole keys/entries. The sparse-matrix represents the tree-nodes where branches diverge, and the string-array the branch values between tree-nodes. Please note that an integer sparse-matrix is a data-structure that computers can process extremely quickly and efficiently.
Taking the 2 colours Magenta and Magnolia the algorithm will create a sparse-matrix row with column 77 (ASCII character 77 is "M") set as a pointer to a string-array entry of "ag". Another sparse-matrix row then takes this further, with columns 101 and 110 (ASCII characters 101 and 110 are "e" and "n") set as pointers to the string-array entries of "nta" and "olia". This is easier understood pictorially :

Picture of the sparse-matrix and string-array teaming-up to produce the STrie tree structure.
The user can explore this within the Colours tab/sheet in the bottom-right quadrant of the downloadable spreadsheet which displays the STrie metadata. The first row of the sparse-matrix has a pointer to row 43 in column 77 (ASCII character 77 is "M"). The branch string-array at row 43 contains "ag", as per the diagram. Also the sparse-matrix at row 43 has pointers to rows 15 and 44 in columns 101 and 110 (ASCII character 101 is "e" and 110 is "n"). Finally the branch string-array at row 15 contains "nta" and at row 44 contains "olia".
If the user then adds 2 additional colours, "Mauve" and "Marigold", then clicks-on the blue metadata row to re-populate the sparse-matrix and string-array, the algorithm will adjust accordingly. It will cut-short the "ag" branch to just "a" (which is common to all 4 colours) and create a new node pointing to "g" for Magenta and Magnolia, "r" for Marigold and "u" for Mauve.
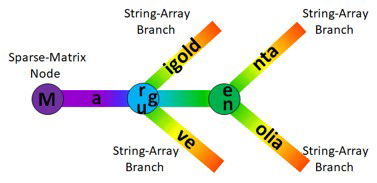
Picture of the sparse-matrix and string-array teaming-up to produce the STrie tree structure.
This is what the STrie algorithm does in its build-phase. The key-understanding is the make-up of the sparse-matrix nodes. They can only ever have a maximum of 256 branches emanating from each node, one for every possible ASCII character. This number is reduced further due to the striping meta-data. This low-number enables a fast linear-scan to operate instead of having to do a binary-search to find a branch. The STrie tree-structure can be represented as a fractal shape (see below), and is shared by the "spectral" universal data-model of symbolic-processors which spawned this algorithm variant. In the read-phase a recursive-procedure constructs the sorted keys/entries from the STrie data-structure.

The STrie Data-Structure: Each violet-to-red line represents a key/entry, each branch represents a string-array entry, and each bend/node represents a sparse-integer-array entry. The violet-to-red colours derive from the "spectral" universal data-model of symbolic processors.
The STrie algorithm has 2 operational-modes that have various names (e.g. indexed/sequential, exact-match/near-match, etc.). The above diagram mirrors this as 2 different ways of locating a branch; either starting from the root and navigating upwards to a leaf, or starting from a leaf and navigating sideways to a successor or predecessor leaf. With STrie the first mode is faster, which mirrors real-world requirements.
4.5. The STrie Speed-Formula
To derive a speed formula for STrie a similar approach is used for those of QuickSort etc. A series of steps is derived for each key/entry, each one consuming an amount of time and resources. In the case of QuickSort these steps were the levels the algorithm went through from partitioning the keys/entries into 2, then 4, then 8 sub-sets and so on. The equivalent for STrie are the branches for each row/entry in the tree (the sub-keys/sub-entries).
The way to calculate the average number of branches in each key/row is first establish the average number of diverging branches at each node in the tree. If on average there were 10 branches per node, and there were 3 levels in a balanced tree, that would result in 1 thousand keys/entries (10 x 10 x 10 = 1000). As QuickSort can only differentiate 2 paths per level, it would require 10 levels (2 * 2 * 2 * 2 * 2 * 2 * 2 * 2 * 2 * 2 = 1024). In this example, assuming the time/effort required at each level is equivalent, it would mean that STrie was over 3 times faster (3 levels instead of 10).
Taking this to the limit, with a maximum number of branches per node-equivalent being 256 for STrie as compared with 2 for QuickSort, gives an 8 fold speed superiority for STrie (2 to the power 8 is 256 representing 8 times less levels required to achieve a certain number of keys/entries to be sorted). This is where the "8 times faster than QuickSort" banner-headline comes from. It is very much an upper limit and has 2 assumptions behind it that should be explored-and-challenged, but the formula O(n/8 log(n)) emerges (to the base 2, for n keys/entries), which is 8 times faster than its competitors.
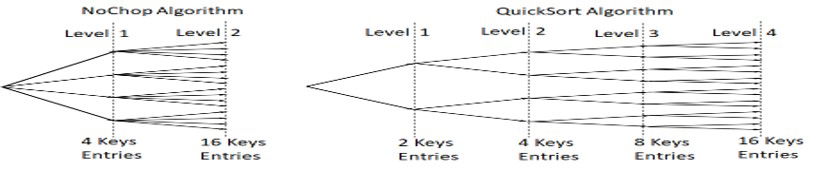
In the 2 tree-structures above we can see STrie with an average of 4 branches per node needing just2 levels to reach 16 keys/entries, but QuickSort needs 4 levels, twice as slow (assuming equal level times per algorithm).
The above picture, and the STrie speed formula in comparison to QuickSort, rest on 2 assumptions. The first assumption is that the processing/time required for each algorithm is equivalent for each key/entry at each level in the algorithm. For QuickSort there is a 50/50 probability it needs to swop 2 keys/entries, which is quite a slow activity. STrie however will often have to do nothing at all at lower levels as there is a match (e.g. in the Colours tab/sheet for a new colour of Mahogany the algorithm needs to do nothing at level 1 as "M" is already loaded in the sparse-matrix and "a" in the string-array). If there is not a match it creates a new branch which is just a part of a key/entry, not the whole key/entry. It is not immediately obvious which algorithm has the bigger time/workload requirements, which is why for the "sake-of-theoretical-argument" they have been "equivalized", leaving empirical analyses to answer the question in practice (i.e. "race" the 2 algorithms to get a feel of the answer).
The second assumption is that there are the same average number of branches-per-node at each level, which is a simplification that allows the upper-limit speed equation for STrie to be derived (using the maximum 256 branches-per-node). Instead there will be a sophisticated probability-distribution, which depending on data, would most probably see higher numbers of branches-per-node at lower levels (e.g. in the Words tab/sheet there are 26 initial branches representing the 26 letters of the alphabet, including "x" for xmas and xrays!). Deriving this probability-distribution is non-trivial and deserving of a white-paper on its own. So the same approach is taken with the previous assumption in that an empirical approach can best illuminate real-world distributions. The metadata in the downloadable spreadsheet includes just such information for each data-set and can be viewed in cells "N1" onwards in the upper-right quadrant of the tab/sheet (note that refreshing the metadata by clicking on the blue metadata-row will take an appreciable amount of time as it has to "dump" both the sparse-matrix and the string-array).
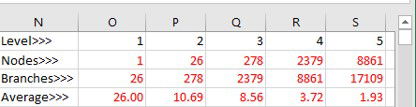
Grid showing the average number of branches per level for the Words tab/sheet.
4.6 Downsides and Watchouts
The STrie algorithm does have a number of considerations to factor-in. The first, as already detailed, is that STrie consumes large amount of computer resources, particularly memory. STrie is at its fastest when there are no other processes competing for memory (the user can/should kill competing processes during trialling). Although the sparse-matrix is large, by modern standards it is "manageable", but poor STrie performance may be due to memory issues (QuickSort uses very little memory as it just swops keys/entries and does not build any metadata).
The second consideration is stability. Stability is a technical issue which concerns itself with whether a sort algorithm can "blow-up" (i.e. encounter data/conditions that are so beyond its safe input "envelope" that run times become excessively long). QuickSort is not stable, but STrie is. The STrie algorithm was designed for data-storage-and-retrieveal, an environment where "no-duplicates-allowed" is the ideal behaviour. Because of this additional code was added to the algorithm to cater for duplicates and inclusions (e.g. Amsterdam is "included" in Amsterdam-Zuidoost). Also the algorithm should be relatively immune from situations that cause excessive run-times as these could only be caused by there being keys/entries made up of tens, hundreds or thousands of levels, each level's processing adding to the run time. However as each level is represented by a minimum of 1 character this would equate to keys/entries being tens, hundreds or thousands of characters long, which for real-world-data they never are.

The number of allowable levels is limited by the maximum length of the keys/entries (the picture to the right shows a 6 level key/entry which is already rather rare for real-world data).
Another very surprising watch-out is that STrie gives a slightly different sort-sequence than QuickSort. After investigation it appears STrie is in-fact correct, but QuickSort is not, for reasons not currently understood (QuickSort was copy-and-pasted from the internet, so AGD Research is not responsible for its veracity). The issue can be seen in the Cities tab/sheet in rows between 22740 and rows 23000. For some reason QuickSort seems to be incorrectly sorting the 2nd character of the key/entry, which happens to be in the "exotic" range (ASCII characters 132 to 255). The ASCII-code for this 2nd character has been included in the adjacent cells so the user can see for themselves (see below the output for QuickSort in this range versus NoChop using the "=CODE(MID(Xnnn, 2, 1))" formula) .

We can see QuickSort (to-the-left) sorting incorrectly, whereas STrie (to-the-right)sorts according to the ASCII sort-sequence.
Finally, in its first iteration STrie contains approximately 200 lines of VBA code as against QuickSort's 30 lines. This reflects the relative complexity of the 2 algorithms (QuickSort just needs to swop keys/entries, but STrie is more sophisticated). With more development it is very likely that the STrie code can be further optimized, especially in a computer language with better control at the chip level (there are commands that do not exist in VBA, such as finding at what position 2 strings begin to differ). Currently however, the supremacy of STrie over QuickSort appears to be 50% on the limited data-sets presented here, which is borderline-compelling. The watchout is that the spreadsheet STrie algorithm accompanying this white-paper should be seen as a proof-of-concept of STrie supremacy, not a finished working version.
5. Future Developments
The "call-to-arms" is for STrie to be progressed from a research stage to a development one. There are 2 clear areas where this can happen:
5.1. Exploiting STrie's Existing Demonstrated Supremacy (replacing current sort algorithms)
Sorting is a ubiquitous process that is necessary in all types of file-systems, databases, platforms, operating systems etc. Typically a sort routine is embedded deep in the software stack so that higher-level applications can call on it and not have a dedicated sort within the application. A programme to replace existing sorts (QuickSort, MergeSort, HeapSort etc.) can be planned to swop this component at an appropriate upgrade point (typically a major release). For new file-systems, databases, platforms and operating systems the STrie algorithm should be chosen immediately as the "sort-of-choice".
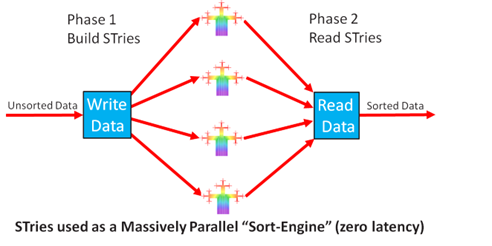
5.2. Exploiting STrie's Potential Massive-Parallelization Supremacy (industrial-scale in-memory sorting, with zero latency)
In returning a sorted sequence of keys/entries there are a number of processing "bottlenecks" including the application overhead, bandwidth concerns and of course the sort algorithm itself. Massive parallelization of STrie can effectively completely remove this last bottleneck (zero latency). This is unlike QuickSort and similar algorithms that require a complete data-set prior to sorting.Note - an exception is InsertSort which does not require a complete data-set prior to sorting, but is not regarded as a leading sort algorithm due to its various "downsides" (e.g. having to "shuffle" entries/keys etc.).
The STrie data-structure is ideally suited to parallelization, the simplest configuration would be for 256 processing-units, each with its own memory, working together. A fast triaging process would send each key/entry to an appropriate processor based on its first character (the ASCII character-set contains 256 symbols). A dedicated series of STries would be built as keys/entries were received, and the end result simply "read-off", lowest-to-highest, once the last one was processed. A more sophisticated triage would balance load more carefully among a configurable number of processing-units (note: the processors could be on different servers and data-centres). Although the STrie sort algorithm on its own already provides a 50+ percent speed supremacy over QuickSort and similar comparison sort algorithms (desirable), the critical differentiator is its suitability for massive parallelization which delivers a zero latency solution (compelling).
6. References
Wikipedia (https://en.wikipedia.org/wiki/Quicksort)
StackOverflow (https://stackoverflow.com/questions/tagged/quicksort)
KhanAcademy (https://www.khanacademy.org/computing/computer-science/algorithms/quick-sort/a/analysis-of-quicksort)
GeeksForGeeks (https:\www.geeksforgeeks.org\quick-sort\)
ResettaCode (https://rosettacode.org/wiki/Sorting_algorithms/Quicksort)
Wikipedia (https://en.wikipedia.org/wiki/Trie)
AGD-Research (https://agdresearch.com/home)
7. Author
Andrew Guthrie-Dow, AGD-Research, January 2025