New & Fun IT, Mathematics, Philosophy, Games & Stories
About
The web-pages are designed to convey a summary understanding. For a detailed understanding there are downloads available on the Downloads web-page. These contain working examples, the computer code (MS VBA), and white-papers.
For a lighter, less techy perspective on AGD Research, additional pages cover amusements, "adult" stories focusing on business-consulting, cannabis and other areas.
Symbolic-processors form a putative new application-type which possesses a universal data-model (the spectral-data-model) A symbolic-processor is a new approach to a new requirement, which in IT "speak"/vernacular is termed a "new-new" solution.
UK/Netherlands based, AGD Research (founded in 1999) provided niche services to the major IT consultancies and fortune-500 companies in the US, Europe and APAC. These services have focused on implementing sophisticated optimization algorithms for supply-chains and value-chains.
AGD Research is also an informal network of consultants and technicians who have worked closely with each other over many years on multiple projects, and whose expertise has been combined and maximized to deliver significant business benefits.
Symbolic-Processor
Goal: A new, simple, single, & universal way of processing data (so commoditizing it)
Problem: A myriad of existing, competing and complex computer-languages
Solution: Extend the universal notation of arithmetic into computer-programming
Mechanism: Adopt the 4 principles below:
1. No Mathematical-Platonism
Traditional computer-languages, and indeed mathematics itself, use symbols to represent underlying objects that exist "out-there", such as integers, reals. bytes etc. These objects can then participate in various operations that again exist "out-there", such as addition, multiplication and concatenation etc.
Unlike this mathematical-Platonism, a symbolic-processor just processes symbols; no pretense is made of any underlying spooky "out-there" reality that they refer to; e.g. the statement abc + def is equally as valid as 123 + 456; it just returns a symbolic-string of zero length (nothing) as compared to the 3 symbol-string (579).
2. Spectral Data-Model
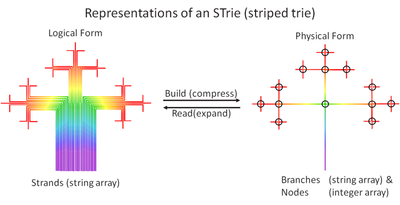
The spectral data-model maps symbolic-strings to physical data-structures and data-stores, whether these be in an application's fast-memory, an underlying file-system or database, on the web, etc. This allows a common way of maintaining data in any application, anywhere, whether it be a spreadsheet, a word-processor, an ERP system, accounting software, B2C retail, or whatever. The accompanying fractal tree-diagram (the pattern repeats itself in ever increasing granularity/resolution) represents the spectral data-model.
Data within a string has left-to-right asymmetry; leading symbols are more "well-known" and represent its key (the how-to-find) and are represented by colours towards the blue-end of the spectrum, while trailing symbols are less "well-known" and represent the record itself (the what-to-find) and are represented by colours towards the red-end of the spectrum.
The spectral data-model is implemented via 2 approaches. Firstly a thin processing layer is introduced at the application level to translate the local data-model (e.g. relational, file-system, spread-sheet etc.) into and out of the spectral data-model. Secondly data within the spectral model is held as a "Trie" data-structure. This data-structure has been optimized via "go-faster-striping" meta-data to deliver maximized performance (see the "Striped-Trie" web-page for details).
3. Combinatory Binary-Operations
With the exception of read-operations which utilize wild-cards and filters, all other operations in a symbolic-processor are binary; they have 1 operator, 2 input operands and 1 output, as in 1 + 2 which returns 3. These operations can be combined in various combinations across symbolic-strings to produce bijections and various Cartesian-products:
1 2 + 3 4 5 returns 1 5 4 5 (example standard)
1 2 ++ 3 4 5 returns 4 6 (example bijection)
1 2 +++ 3 4 5 returns 13 14 (example Cartesian-accumulate)
1 2 ++++ 3 4 5 returns 4 8 13 5 9 14 (example Cartesian-carry)
1 2 +++++ 3 4 5 returns 4 5 6 5 6 7 (example Cartesian-classic)
4. No Explicit Loops, Routines or If/Then Statements
The functionality above almost-entirely removes the need for a symbolic-processing-language to have explicit loops, routines or if/then statements. More fundamental operations (comparison and replication) can be used to provide this implicit functionality if required.
Details
For a detailed understanding there are downloads available on the Downloads web-page. These contain working examples, the computer code (MS VBA), and white-papers. In an example of determining the standard-deviation of a sample-set the number of lines-of-code is reduced from 25 in "C" to just 5 in SPL (symbolic-processing-language).


Striped-Trie
Goal: A trie data-structure optimized for use in the spectral data-model & other applications (e.g. data sorting, retrieval & maintenance etc.)
Problem: Standard tries are inefficient at data-storage and sub-optimal in near key/entry matching
Solution: Minimize data-storage and maximize near key/entry location performance
Mechanism: A 256 bit ascii pointer vector approach in combination with meta-data striping/clustering
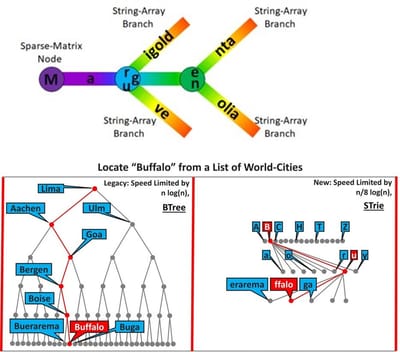
The first accompanying trie diagram of 4 colours has 3 nodes and 6 branches (one of which is empty). Navigating from the root-node outwards through all the branches and sub-nodes returns the 4 colours "Marigold, Magenta, Magnolia and Mauve" (the 4 keys/entries) as a sorted sequence.
In general, if n is the number of keys/entries and n+ the number of nodes, the nodes are represented as a 256 bit ascii pointer vector ("IT-speak"!). In perhaps simpler-but-equivalent "math-speak", they are represented as a sparse 2-dimensional integer matrix of n+ rows (the nodes) and 256 columns (the ascii character-set). This forms a "DNA" sequence of characters/symbols that navigates from the root-node outwards and reconstructs each individual key/entry.
The second accompanying diagram demonstrates STrie's superiority over BTree in that having multiple branches per node results in less processing levels being required to locate a key/entry. The maximum of 256 branches for each node results in 8 times fewer levels (2 ^ 8 = 256), giving a rough-and-ready speed-limiter of n(log (n) / 8 in "big O" notation; 8 times faster.
Branches are represented as a 1-dimensional string-array of n+ rows. This forms a "junk-DNA" sequence of characters/symbols which do not affect the "node-navigation", but do contribute to the reconstruction of the key/entry. This "junk-DNA" usually comes at and/or near the end of keys (e.g. "ffalo" in "Buffalo"), but can occur anywhere (e.g. "est " in "West Carson" and "West Chester"). If a row-pointer is non-zero its column-position represents the ascii code concerned (e.g. a 123 in column 102 means "B"s are located in row 123, and a 4567 in column 165 means "u"s are located in row 4567).
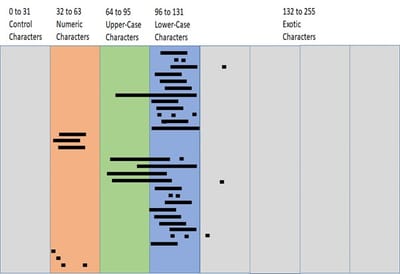
The third accompanying striping/clustering diagram shows how the sparse integer matrix is refined by meta-data which indicates where non-zero row-pointers occur within the nodes (i.e. "where the action is"). The vertical stripes partition the ascii character-set into like-bands where data tends to cluster (e.g. alphabetics, numbers, etc.). The horizontal lines and points demarcate within each node where the data actually clusters which minimizes the number of linear-scans required. In this implementation if there are 3 or less row-pointers they are represented as point-vectors (e.g. "r", "g" and "u"), otherwise they are represented as a range-vector and a single point-vector (e.g. "B to Q" and "Z").
This approach is essential to maximize near key/entry location performance which is required to out-compete current algorithms that sort, retrieve and maintain data (e.g. QuickSort, BinarySearch and BTree etc.). These are required for applications such as symbolic-processors, sort-engines, spell-checkers and text-auto-fillers, dictionaries, relational and NoSQL databases, file-systems, etc.
The Downloads web-page contains working-examples and white-papers of STrie versus QuickSort (50+ percent faster), STrie versus BinarySearch (350% faster) and STrie versus BTree (100+ percent faster). The proof-of-concept code is written in MS VBA which was chosen for its ability to seamlessly integrate with Excel.
Although these are significant the compelling differentiator of the algorithm is its suitability for massive parallelization. Both data and processing can easily be spread across CPUs. The simplest way of doing this would be to front-end the algorithm with a triaging routine that distributes data (and hence processing) to 1 of 256 CPUs, based on the initial character of the STrie. A more sophisticated triaging routine would better-balance loads based on usage criteria.
File-Downloads
Download (to .zip compressed-format), unzip (to .xslm Excel/VBA-format), allow security if required (right-click on the file in file-editor, select Properties, then click the Security-Unblock box), open the file and respond to the "Enable" prompt(s). The user can first view the overview, tabs and white-paper safely (decline "Enable"), before enabling algorithms/VBA (accept "Enable"). Compatible with both 32 and 64 bit pc's.
Symbolic-Processor
Proof-of-Concept (command-line) & Theory (white-paper). Version 16.
STrie-vs-QuickSort
Proof-of-Concept (command-line) & Theory (white-paper). Version 16.
STrie-vs-BinarySearch
Proof-of-Concept (command-line) & Theory (white-paper). Version 16.
STrie-vs-BTree
Proof-of-Concept (command-line) & Theory (white-paper). Version 16.
White-Papers
This white-paper explores the use the STrie data-structure and algorithm in sorting data, and compares it to the industry standard, Quick-Sort.
Read MoreThis white-paper explores the use the STrie data-structure and algorithm in retrieving data, and compares it to the industry standard, Binary-Search.
Read MoreThis white-paper explores the use the STrie data-structure and algorithm in maintaining data, and compares it to the industry standard, BTree.
Read MoreProfessional Services
To join the conversations surrounding Symbolic-Processors and supply-chain/value-chain optimization please contact AGD Research directly via the Contact web-page. To explore resourcing options please contact the above associate-organizations directly.

3x3
3x3 is so simple-to-play it actually easier to explain in a single paragraph of words rather than pictures. Take a pack-of-cards, and if it has no jokers, remove/discard a single court-card (jack, queen or king), then shuffle it. Then turn-over the top card, and place it in an empty "square" anywhere you like in a 3x3 grid (hence the name!), and continue until the grid is full. If at any time the sum of cards in a row, column or diagonal add-up to a number that is divisible by five, they can be removed from the grid (court-cards and jokers count as 10). You win if all the cards from the deck and grid are removed, otherwise you lose. The accompanying diagrams show an example game of 3x3 utilizing some common tactics and strategies.
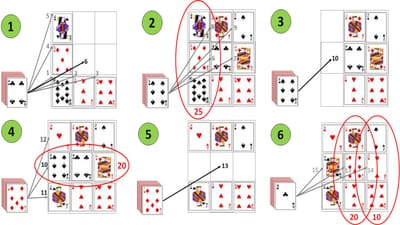
In-diagram-1 the grid is being filled from the left-to-right, bottom-to-top. The queen is placed out-of-sequence in the top-left "square" as this ensures the sum-of-cards in the first-column is divisible by five (10 + 5 + 10 = 25 = 5 x 5). In-diagram-2 the rest of the grid is populated left-to-right, bottom-to-top. In-diagram-3 the cards in the first-column are then removed/discarded.
In-diagram-4 the first-column is then re-populated, with the six immediately placed in the centre as this ensures the sum-of-cards in the middle-row is divisible by five (6 + 4 + 10 = 20 = 5 x 4). In-diagram-5 the cards in the middle-row are then removed/discarded.
In-diagram-6 the middle-row is then re-populated, with the seven immediately placed at the centre as this ensures the sum-of-cards in the middle-column is divisible by five (3 + 7 + 10 = 20 = 5 x 4). The two is then placed to the right as this ensures the sum-of-cards in the right-row is also divisible by five (4 + 2 + 2 = 10 = 5 x 2), before the king is placed to the left.
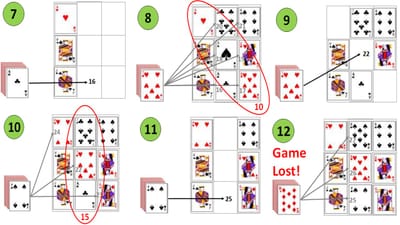
In-diagram-7 the cards in the middle-and-right-rows are then removed/discarded. In-diagram-8 the middle-and-right-rows are then re-populated, left-to-right, bottom-to-top, and somewhat-luckily, the sum-of-cards in the backslash-diagonal is divisible by five (1 + 1 + 8 = 10 = 5 x 2). In-diagram-9 the cards in the backslash-diagonal are then removed/discarded.
In-diagram-10 the backslash-diagonal is then re-populated, with the seven immediately placed at the centre as this ensures the sum-of-cards in the middle-column is divisible by five (1 + 7 + 7 = 15 = 5 x 3). In-diagram-11 the cards in the middle-column are then removed/discarded. In-diagram-12 the middle-column is then re-populated, bottom-top. Unfortunately this results in no rows, columns or diagonals being divisible by 5, and the game is lost.
The above example highlights some tactics and strategies that can increase the chances of winning the game, including planning to remove horizontal and vertical rows alternatively, and being aware that cards that count as ten are much more common than others. Also, placing a card that is divisible by five in the central "square" creates four opportunities for cards that count as five or ten to complete a removable threesome (1 row, 1 column and 2 diagonals), whereas placing it in a corner creates three opportunities (1 row, 1 column and 1 diagonal), leaving just two opportunities anywhere else (1 row and 1 column). An additional strategy is card counting; cards that are removed/discarded will weight the likelihood of subsequent ones having a different value.
The game can be made easier-or-harder by subtlety changing the rules. The easiest game includes the divisor being five, diagonals being removable, and the grid can migrate (i.e. if there are just two rows populated, the re-populated row can be placed above or below them, and likewise for columns). With these lax rules in-place, and with significant-player-experience, leads towards fifty-percent of games being winnable.
The hardest game includes the divisor being ten, diagonals not-being removable, and the grid cannot migrate (i.e. if there are just two rows populated, re-population can only occur in the empty-row, and likewise for columns). With these stringent rules in-place, winning is a significant challenge!
What the optimal tactics and strategies are, and the resulting likelihood of winning the game, is a non-trivial mathematical calculation that the author has not even attempted to ascertain!
Finally, the author would like to encourage anyone who wants to create a digital version of this game, playable online via your pc or phone. All copyright is waved.
Andrew Guthrie-Dow, January 2025
Consulting-Stories
Of the thousands of rides undertaken by AGD-Research to conduct business, this is the most memorable for all the "wrong" reasons.
Read MoreThis story follows a "day-in-the-life" of a sales-consultant and focuses on a particular car journey to-and-from the prospect.
Read MoreOf the thousands of rides undertaken by AGD-Research to conduct business, this is the most memorable for all the "right" reasons.
Read MoreHere I describe visiting Kabukicho in Shinjuku-East, central Tokyo twice, once in the 90's and again twenty years later, and learning at first-hand how that justifiably famous red-area has evolved.
Read MoreCannabis-Tales
Travelling can be relaxing, and no more-so when boosted by a little (or a lot) of cannabis - well most of the time!
Read MoreCannabis and sex; a great combination. Not only does it turbo-charge your excitement-and-satisfaction whatever your sexuality, it can also lead to some very "interesting" experiences.
Read MoreSM-101
This sets-out the SM/fetish "landscape" from the stance that they're great-fun (trust me on this). Due to massive popular demand (thanks Michael) this introduction is followed by personal experiences.
Read MoreThis is our SM discovery-phase (in project-management "speak" this is where you uncover what you are dealing with before proceeding).
Read MoreRants-&-Rambles
L.Bear
One story of how L.Bear (Little-Bear) follows and achieves his goal of self-improvement.
Read MoreKnowing what type of bear you have is critically important - to you, the bear, and society itself!
Read MoreHow Bear's obsession with gold derailed the Bank-of-England.
Read MoreHow Little-Bear needed more than just financial-success. He now wanted to explore the deep-value of a traditional Xmas.
Read MoreContact